目录
七年级数学(上)知识点
人教版七年级数学上册主要包含了有理数、整式的加减、一元一次方程、图形的认识初步四个章节的内容.
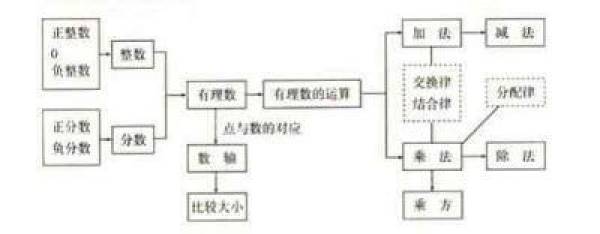
第一章 有理数
一、知识框架
二、知识概念
1.有理数:
q(p,q为整数且p,0)
(1)凡能写成形式的数,都是有理数。正整数、0、负整数统称整数;
正分数、负分数统称分数(有限小数和无限循环小数);
整数和分数统称有理数.
注意:0即不是正数,也不是负数;
-a不一定是负数,+a也不一定是正数;
,不是有理数,是无限不循环小数;
,,正整数,正整数,正有理数,,,,整数零正分数,,,,
(2)有理数的分类: ? ? ,负整数有理数有理数零,,,,,负整数,正分数,负有理数分数,,,,负分数负分数,,,,
2.数轴:
数轴是规定了原点、正方向、单位长度的一条直线.
3.相反数:
(1)只有符号不同的两个数,我们说其中一个是另一个的相反数;0的相反数还是0;
(2)相反数的和为0 , a+b=0 , a、b互为相反数.
4.绝对值:
(1)正数的绝对值是其本身,0的绝对值是0,负数的绝对值是它的相反数;
注意:绝对值的意义是数轴上表示某数的点离开原点的距离;
a(a,0),a(a,0),,a,a,0(a,0)(2) 绝对值可表示为:或绝对值的问题经常分类讨论; ,,,a(a,0),,,a(a,0),
5.有理数比大小:
(1)正数的绝对值越大,这个数越大;
(2)正数永远比0大,负数永远比0小;
(3)正数大于一切负数;
(4)两个负数比大小,绝对值大的反而小;
(5)数轴上的两个数,右边的数总比左边的数大; (6)大数-小数 , 0,小数-大数 , 0.
6.互为倒数:
乘积为1的两个数互为倒数;注意:0没有倒数;
1a若 a?0,那么的倒数是;若ab=1, a、b互为倒数;若ab=-1, a、b互为负倒数. a
7.有理数加法法则:
(1)同号两数相加,取相同的符号,并把绝对值相加; (2)异号两数相加,取绝对值较大的符号,并用较大的绝对值减去较小的绝对值;
(3)一个数与0相加,仍得这个数.
8.有理数加法的运算律:
(1)加法的交换律:a+b=b+a ;
(2)加法的结合律:(a+b)+c=a+(b+c).
9.有理数减法法则:
减去一个数,等于加上这个数的相反数;即a-b=a+(-b).
10.有理数乘法法则:
(1)两数相乘,同号为正,异号为负,并把绝对值相乘;
(2)任何数同零相乘都得零;
(3)几个数相乘,有一个因式为零,积为零;各个因式都不为零,积的符号由负因式的个数决定.
11.有理数乘法的运算律:
(1)乘法的交换律:ab=ba;
(2)乘法的结合律:(ab)c=a(bc)
(3)乘法的分配律:a(b+c)=ab+ac
12.有理数除法法则:
除以一个数等于乘以这个数的倒数;注意:零不能做除数,即无意义0
13有理数乘方的法则:
(1)正数的任何次幂都是正数;
(2)负数的奇次幂是负数;负数的偶次幂是正数; (nnnnnn nn注意:当n为正奇数时: (-a)=-a或(a -b)=-(b-a) , 当n为正偶数时: (-a) =a或 (a-b)=(b-a) .
14.乘方的定义:
(1)求相同因式积的运算,叫做乘方;
(2)乘方中,相同的因式叫做底数,相同因式的个数叫做指数,乘方的结果叫做幂; n
15.科学记数法:
把一个大于10的数记成a?10的形式,其中a是整数数位只有一位的数,这种记数法叫科学记数法.
16.近似数的精确位:
一个近似数,四舍五入到那一位,就说这个近似数的精确到那一位.
17.有效数字:
从左边第一个不为零的数字起,到精确的位数止,所有数字,都叫这个近似数的有效数字.
请判断下列题的对错,并解释.
1.近似数25.0的精确度与近似数25一样. 错。前者精确到十分位(小数点后面一位),后者精确到个位数。
2.近似数4千万与近似数4000万的精确度一样. 错。4千万精确到千万位,4000万精确到万位。
3.近似数660万,它精确到万位.有三个有效数字. 对。
4.用四舍五入法得近似数6.40和6.4是相等的. 错。值虽然相等,但是取之范围和精确度不同
5.近似数3.7×10的二次与近似数370的精确度一样. 错。3.7×10^2精确到十位,370精确到个位
相关概念:
有效数字:是指从该数字左边第一个非0的数字到该数字末尾的数字个数(有点绕口)。
举几个例子:3一共有1个有效数字,0.0003有一个有效数字,0.1500有4个有效数字,1.9*10^3有两个有效数字(不要被10^3迷惑,只需要看1.9的有效数字就可以了,10^n看作是一个单位)。
精确度:即数字末尾数字的单位。比如说:9800.8精确到十分位(又叫做小数点后面一位),80万精确到万位。9*10^5精确到10万位
18.混合运算法则:
先乘方,后乘除,最后加减.
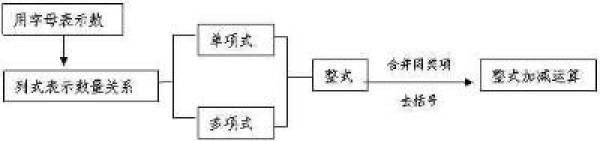
第二章 整式的加减
一、知识框架
二、知识概念
1.单项式:在代数式中,若只含有乘法(包括乘方)运算。或虽含有除法运算,但除式中不含字母的一类代数式叫单项式.
2.单项式的系数与次数:单项式中不为零的数字因数,叫单项式的数字系数,简称单项式的系数;系数不为零时,单项式中所有字母指数的和,叫单项式的次数.
3.多项式:几个单项式的和叫多项式.
4.多项式的项数与次数:多项式中所含单项式的个数就是多项式的项数,每个单项式叫多项式的项;多项式里,次数最高项的次数叫多项式的次数。
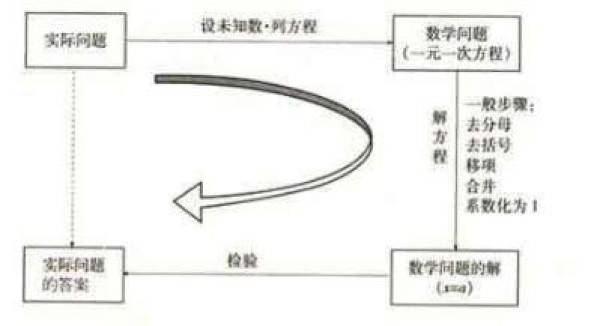
第三章 一元一次方程
一、知识框架
二、知识概念
1.一元一次方程:只含有一个未知数,并且未知数的次数是1,并且含未知数项系数不是零的整式方程是一元一次方程.
2.一元一次方程的标准形式: ax+b=0(x是未知数,a、b是已知数,且a?0).
3.一元一次方程解法的一般步骤: 整理方程„去分母„去括号„移项„合并同类项„系数化为1„(检验方程的解).
4.列一元一次方程解应用题:
1)读题分析法:„„„„ 多用于“和,差,倍,分问题” (
仔细读题,找出表示相等关系的关键字,例如:“大,小,多,少,是,共,合,为,完成,增加,减少,配套—–”, 利用这些关键字列出文字等式,并且据题意设出未知数,最后利用题目中的量与量的关系填入代数式,得到方程.
(2)画图分析法: „„„„ 多用于“行程问题”
利用图形分析数学问题是数形结合思想在数学中的体现,仔细读题,依照题意画出有关图形,使图形各部分具有特定的含义,通过图形找相等关系是解决问题的关键,从而取得布列方程的依据,最后利用量与量之间的关系(可把未知数看做已知量),填入有关的代数式是获得方程的基础.
(3)列方程解应用题的常用公式:
(1)行程问题: 距离=速度?时间 时间,速度,时间速度
(2)工程问题: 工作量=工效?工时 工时,工效,工效工时
(3)比率问题: 部分=全体?比率 全体,比率,比率全体
(4)顺逆流问题: 顺流速度=静水速度+水流速度 逆流速度=静水速度-水流速度
(5)商品价格问题:售价=定价?折? ,利润=售价-成本, ; 利润率
(6)周长、面积、体积问题:C=2πR,S=πR,C=2(a+b),S=ab, C=4a,2S=a,S=π(R-r),V=abc ,V=a,V=πRh ,V=πRh.
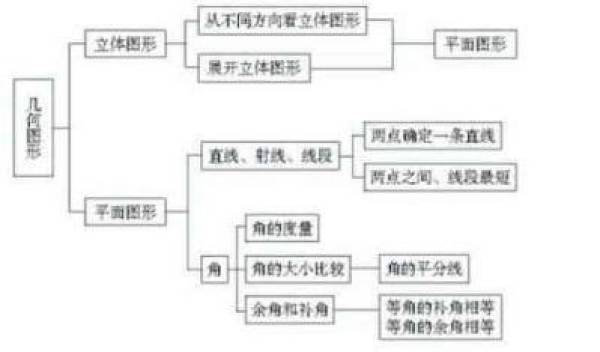
第四章 图形的认识初步
一、知识框架
二、知识概念
1.分类讨论思想: 在过平面上若干个点画直线时,应注意对这些点分情况讨论;在画图形时,应注意图形的各种可能性。
2.方程思想:在处理有关角的大小,线段大小的计算时,常需要通过列方程来解决。
3.图形变换思想:在研究角的概念时,要充分体会对射线旋转的认识。在处理图形时应注意转化思想的应用,如立体图形与平面图形的互相转化。
4.化归思想:在进行直线、线段、角以及相关图形的计数时,总要划归到公式n(n-1)/2的具体运用上来。